Permanent Tide Systems

On this page:

Permanent Tide

The gravity of the Moon and the Sun (and the other planets) not only cause ocean tides, but also a displacement of the Earth's crust known as solid earth tides, with a main component of meter-level amplitude at periods of 12 hours and longer. Although the gravitational force causing earth tides and ocean tides is the same, the responses are quite different. And apart from the direct effect on the Earth's gravity field, there is also an indirect effect caused by the elastic deformation of the Earth.

The tide-generating potential of the Moon and the Sun averaged over a long time are not zero, because the apparent motion of the Moon and the Sun is rather close to the Earth's equator. This is called the permanent tide effect, high in the equatorial zone and low in the polar zones. To deal with the permanent deformation this causes, there are three concepts that are available for the potential field quantities of the Earth (gravity and geoid) and two concepts for the 3-D shape of the Earth (also called crust), described in the rotating Earth-fixed coordinate system. Note that the instantaneous solid earth tides consist of the permanent tide effect together with the time-dependent (periodic) tide effects.

Tide Systems

Tide System	Direct Permanent Tide Effect	Indirect Deformation Effects	Characteristics
mean-tide	retained	retained	The permanent tide effect of the Moon and the Sun is not removed from the potential field quantities (gravity and geoid), nor from the shape of the Earth (crust). Both mean gravity and the mean geoid retain the tide-generating potential (the direct effect) and the potential of the permanent tidal deformation of the Earth (the indirect effect). The mean crust corresponds to the long-time average under tidal forcing. This concept is the most natural one for users.
zero-tide	removed	retained	The tide-generating potential is removed from zero gravity and the zero geoid, but the indirect tidal deformation effect is retained. For the shape of the Earth its logical partner is the mean-tide system. Instead of separately specifying "zero for geopotential, mean for 3-D", the terminology is adopted that for the crust we have zero crust ≡ mean crust. In this alternative, the gravity field is generated only by the masses of the Earth (plus the centrifugal force).
tide-free (non-tidal)	removed	removed	Both the tide-generating potential of the Moon and the Sun and the tidal deformation potential of the Earth are removed from tide-free gravity and the tide-free geoid. The permanent tidal deformation is also removed from the tide-free crust. This corresponds to physically removing the Sun and the Moon to infinity. Conventionally, the permanent deformation is treated using the same Love numbers h and k and Shida number l as for the time-dependent tidal effects, instead of estimates for secular (fluid or "realistic") numbers. This concept is based on models only and is far away from the real Earth shape.

Conversions

The differences of these three gravity fields can be described (as the gravity field itself) in terms of spherical harmonics. Strictly, these spherical harmonic series go up to infinity. But because the permanent tidal effects (averaged over a long time) change the gravity field only very globally, it turns out that it is sufficient (to 1 mm) to change only the C₂₀ term, which describes the flattening of the equipotential surfaces of the gravity field. Conceptually, one would get a mean-tide ellipsoid, a zero-tide ellipsoid, and a tide-free ellipsoid, each with a different equatorial radius and flattening. However, if the reference ellipsoid is treated as a purely geometric quantity, unchanged by permanent tide systems, and only the geoid itself is allowed to change due to the permanent tide systems, then the geoid undulation also changes from one tide system to another, by a zonally uniform correction.

CODE

N (mean-tide) - N (zero-tide) = - 0.198 * ( 3/2 * sin(phi)^2 - 1/2 )             = ( + 0.099 - 0.296 * sin(phi)^2 )               [m]
N (zero-tide) - N (tide-free) = - 0.198 * ( 3/2 * sin(phi)^2 - 1/2 ) *   k       = ( + 0.099 - 0.296 * sin(phi)^2 ) *   k         [m]
N (mean-tide) - N (tide-free) = - 0.198 * ( 3/2 * sin(phi)^2 - 1/2 ) * ( k + 1 ) = ( + 0.099 - 0.296 * sin(phi)^2 ) * ( k + 1 )   [m]

The zero frequency Love number k must be adopted because it is fundamentally unknowable. For EGM96 and EGM2008, k = 0.30 was adopted. The IERS Conventions (2010) give k₂₀ = 0.29525 for the elastic Earth model and k₂₀ = 0.30190 for the anelastic Earth model.

In the Conventions for the Definition and Realization of a European Vertical Reference System (EVRS) a formula is given for the normal height:

CODE

H*(zero-tide) - H*(mean-tide) = + 0.09940 - 0.29541 * sin(phi)^2 - 0.00042 * sin(phi)^4   [m]

Current Practice

According to the IAG resolutions 9 and 16 adopted in Hamburg 1983, the indirect effect due to the permanent yielding of the Earth must not be removed. It therefore requires the zero-tide system for the gravity field (geoid) and the zero-tide ≡ mean-tide system for the 3-D Earth (crust).

However, current practice for 3-D positioning is tide-free – the permanent part of the tidal deformation is not restored. Coordinates in the International Terrestrial Reference Frame ITRFxx, and through it all modern continental and national reference coordinates (for example those given in the European Terrestrial Reference system ETRS89) are in the conventional tide-free system. Tide systems used for potential differences determined with precise leveling are mixed (overwhelmingly mean-tide).

This current practice dates back to the time when tidal corrections were introduced in the 1940s to improve the precision of geodetic measurements. In many cases their implications for the reference systems and reference frames dawned on geodesists much later. At the first stage of tidal ("luni-solar") corrections, the conventional tide-free systems were the almost inevitable outcome. The tide-free approach seems to have entered the 3-D reference frames more or less by accident (not by design), through the processing programs of the observations (VLBI, SLR, GPS). That apparently happened despite the recommendations of the IERS processing standards for the zero-tide ≡ mean-tide system. Attempts in the 1990s to go over to the mean system for the global 3-D reference frames were abandoned after strong protests from users.

Current practice for gravity is zero-tide. It appears that all modern reference gravity values since about 1988 are in the zero-tide system. Geopotential models, i.e., Earth Gravitational Models (EGMs), are nowadays usually provided both in conventional tide-free and in zero-tide versions as far as the potential coefficients are concerned. The difference is only in the J₂ or C₂₀ term. Note that the EGMs are to be evaluated at (conventional) tide-free coordinates. Regional gravimetric geoid models in the past often inherited their tidal systems implicitly from the EGM used, but nowadays are usually explicitly stated to be in the zero-tide system. Note that gravity field modelling is not possible in the mean-tide system because the gravity potential would not be a harmonic function.

Legacy national height systems are overwhelmingly in the mean-tide system, i.e., mean crust over the mean geoid. This has usually not been by design: if no "luni-solar" correction is applied to precise leveling, then the mean system emerges automatically. The luni-solar correction when applied has almost invariably (and unwittingly) resulted in a conventional tide-free system (tide-free crust over tide-free geoid). New national zero-tide systems adopted since 2005 are zero-tide (mean crust over zero geoid).

Regarding continental and global height systems, the European Vertical Reference System (EVRS) is zero-tide by definition, but due to the mixed systems (mostly mean, some non-tidal) of the national observations going into the United European Leveling Network UELN-95/98, its first realization EVRF2000 was mixed. Later realizations EVRF2007 and EVRF2019 were computed in the zero-tide system. The results of EVRF2019 are additionally provided in the mean-tide system – together with the comment to use these heights for tasks of oceanography as well as for clock rates. The mean-tide heights can also be used in the future for comparison with heights in the International Height Reference System (IHRS), which will be provided in the more natural mean-tide system according to the IAG resolution 1 adopted in Prague 2015.

In satellite altimetry of the oceans, the Geophysical Data Records (GDRs) by the operating agencies typically provide the range from the satellite to the instantaneous sea surface, the height of the satellite above a reference ellipsoid, tidal corrections that do not remove the permanent tide, and geoid heights of an EGM in the mean-tide system, relative to the field of the reference ellipsoid (for example the TOPEX/Poseidon datum). Calculations with the quantities in the GDR thus give the height of the sea surface relative to a mean geoid. Mean Sea Surface (MSS) models, constructed from multi-mission altimetry data, refer the surface either to an ellipsoid, or to an EGM geoid in the mean-tide system, though the tidal system of the geoid is not always explicitly stated in the documentation.

EPSG Dataset

In December 2020, the EPSG Geodetic Parameter Dataset added two separate vertical datums for the European Vertical Reference Frame 2019, one with the post-fix "mean tide", i.e., EPSG:1287, and one without a post-fix, i.e., EPSG:1274, which apparently indicates the zero-tide system now. Note that (most) other datums are in the conventional tide-free system.

The difference between the two tide system datums is given as a difference between geopotential numbers, which can be converted to normal heights:

CODE

C (mean-tide) - C (zero-tide) = + 0.28841 * sin(phi)^2 + 0.00195 * sin(phi)^4 - 0.09722 - 0.08432   [kgal m]
H*(mean-tide) - H*(zero-tide) = + 0.29541 * sin(phi)^2 + 0.00042 * sin(phi)^4 - 0.09940 - 0.08593   [m]

The additional offset of 0.08432 kgal m or 0.08593 m forces the mean-tide height to the zero-tide height in NAP at the EVRF2000 origin in Amsterdam.

Datum transformations between national heights and the two EVRF2019 heights are defined using grid interpolation files, i.e., 'nl_2019m' for the transformation between NAP height and EVRF2019 mean-tide height and 'nl_2019z' for the transformation between NAP height and EVRF2019 [zero-tide] height.

Orthometric Heights

An important application of the geoid undulation N is the determination of the orthometric height H of a point from the ellipsoidal height h.

CODE

H = h – N

The H value will be given with respect to the geoid whose undulations, with respect to a specific ellipsoid, are given by N. It is clear that h and N must be given in a consistent tide system. Although the difference between heights in a tide-free and zero-tide system are on the order of 10 cm, it is important for consistency purposes that h and N be given in the same system.

Mean Sea Surface Models

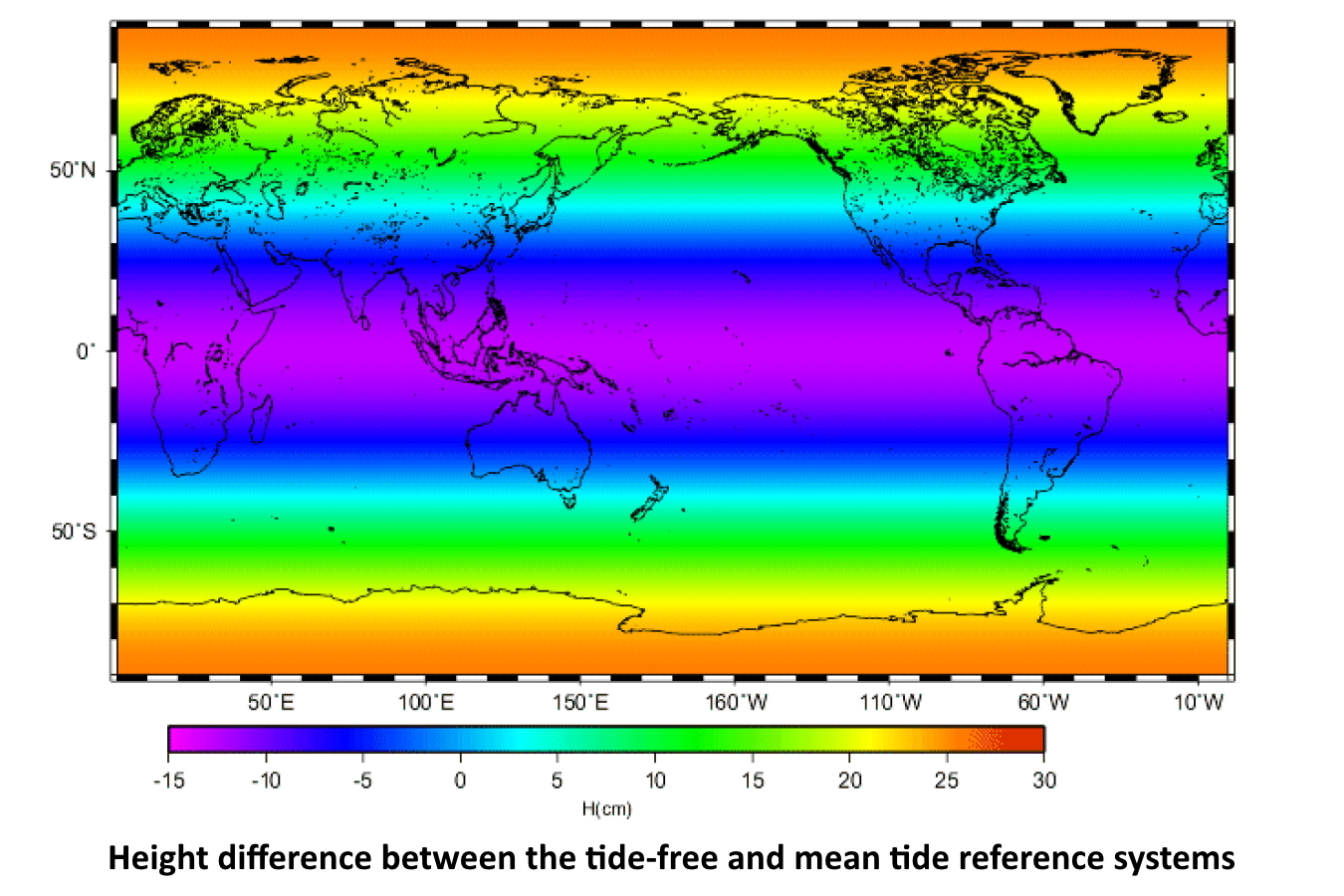
As mentioned above, MSS models are defined relative to the mean-tide system, and geoid models are defined relative to the tide free system. When computing an ocean Mean Dynamic Topography (MDT), the MSS and the geoid first have to be computed in the same system. If not, the impact on the resulting MDT is large: for instance, the figure below, from the GOCE User Toolbox (GUT) Tutorial published by ESA, shows the difference between the tide-free and the mean-tide reference systems.

Sources

Dru A. Smith (1998), There is no such thing as "The" EGM96 geoid: Subtle points on the use of a global geopotential model. In: IGeS Bulletin 8, International Geoid Service, Milan, Italy.
Ihde J., Mäkinen J., Sacher M. (2009), Conventions for the Definition and Realization of a European Vertical Reference System (EVRS) – EVRS Conventions 2007. EVRS website.
Mäkinen J., Ihde J. (2009) The Permanent Tide In Height Systems. In: Sideris M.G. (eds) Observing our Changing Earth. IAG Symposia, volume 133. Springer, Berlin, Heidelberg.
Mäkinen J. (2020). The permanent tide and the International Height Reference Frame IHRF. Preprint.
Poutanen, M., Vermeer, M., Mäkinen, J. (1995) The permanent tide in GPS positioning. Journal of Geodesy 70. Springer, Berlin, Heidelberg.
Petit G., Luzum B., eds. (2010). IERS Conventions (2010). IERS Technical Note 36, Observatoire de Paris, Paris. IERS website.
Ambrózio, A. (2016), GUT TUTORIAL. European Space Agency (ESA). ESA website.