Fledermaus Create Mesh Wizard
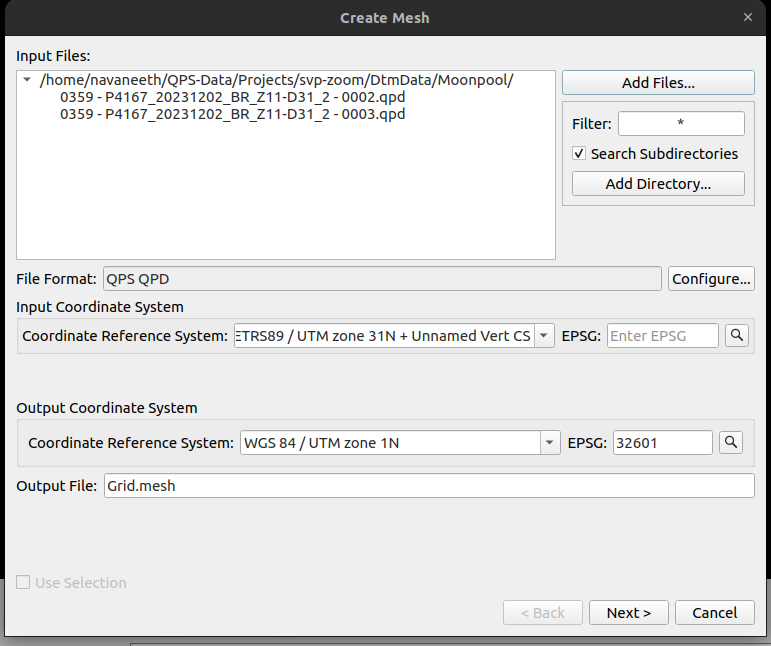
Create Mesh Wizard - Page 1
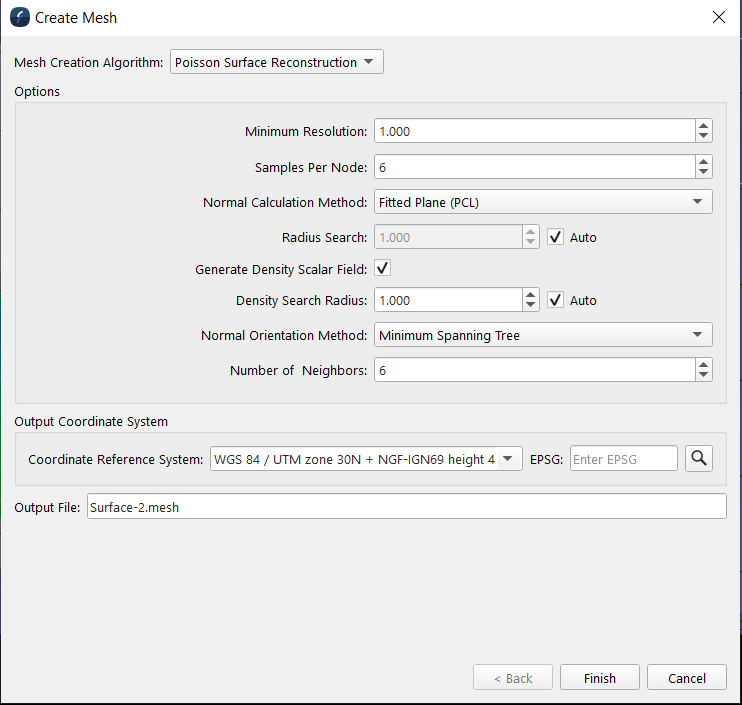
Create Mesh Wizard - Page 2
How to Start
- Main Menu Bar → Create → Create Mesh
- Scene Objects Dock → Right-Click on point cloud object (.points) → Operations → Create Mesh
- Scene Objects Dock → Operations → Create Mesh
Create Mesh Wizard from Create Menu
What it Does
The Create Mesh Wizard allows the user to create a mesh surface on a selected area with specified settings.
Normals Utilized for Creating a Mesh
If the mesh was created out of a point cloud by right clicking on a points object >> operations >> Create mesh, the field Normals is going to be added to the aforementioned object so that the user could color by the normals that were used as input to the mesh creation algorithm as the following figure illustrates.
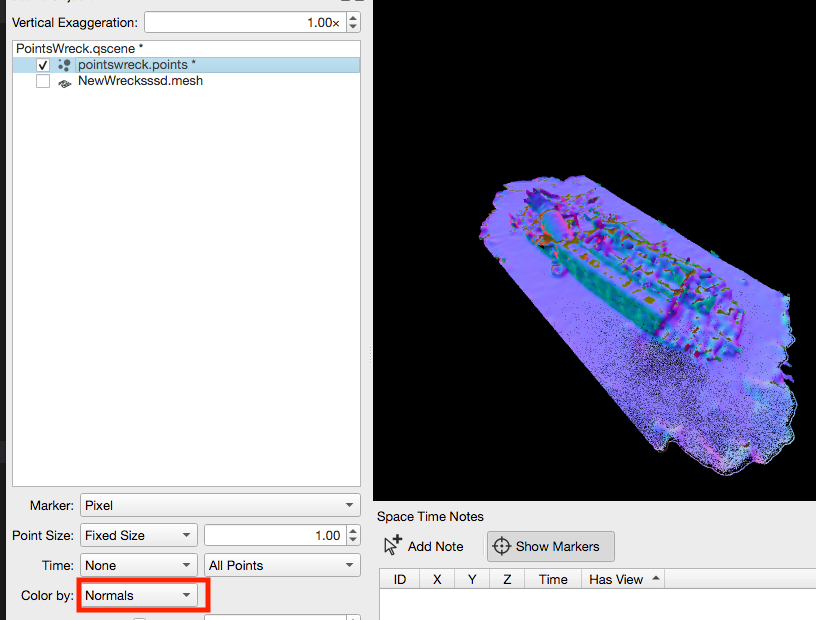
General Description
Mesh Creation Algorithm
Poisson Surface Reconstruction
Reconstructs a triangle mesh from a set of oriented 3D points by solving a Poisson system.
Delauney Triangulation
This is a very fast algorithm that creates a 2.5D triangulated surface.
When choosing the Delauney Triangulation Algorithm, the only customization setting that is changeable is the Output File name. The rest of the settings are set for the creation of the mesh.
Options
Depending on your choice of Algorithm you may be presented with a number of the following mesh creations options:
Minimum Resolution
This is the target width of the finest level of tree cells that will be used for surface reconstruction. A lower value will result in a higher resolution mesh.
Samples Per Node
This value specifies the minimum number of sample points that should fall within an octree node as the octree construction is adapted to sampling density. For noise-free samples, small values in the range [1.0 - 5.0] can be used. For more noisy samples, larger values in the range [15.0 - 20.0] may be needed to provide a smoother, noise-reduced, reconstruction.
Normal Calculation Method
A "normal" is a line or vector that is perpendicular to a given object. In 3D graphics it is most often used for calculating reflections on a surface. For our application, we are calculating the normal for each point, in an effort to identify what should be the inside or outside of the final surface. The normal directions have a large effect on the final mesh that is created, as the Poisson algorithm will try to create a surface that consistently wraps around the points, forming a complete surface. When you have adjacent points with very different normals, the final surface will either be fragmented, or have large "bubbles" as the surface wraps around itself. There are two options available.
Fitted Plane (PCL)
This algorithm which comes from the Point Cloud Library (PCL) attempt to fit a localized plane around the point of interest based on its neighbors. This is the default choice.
Quick Neighborhood Algorithm
This algorithm looks at the neighbors and attempts to produce normals that would point in a consistent direction.
Radius Search
This value specifies the size of a sphere around each point for which other points are included when the PCL normal algorithm is being used. Normally this value is automatically calculated but one can override it if desired.
Generate Density Scalar Field
This option calculates the number of input points that contribute to the final surface triangles, using the "Radius Search" value as a maximum distance. The density value is very useful for cropping out parts of the mesh that were created from a low number of points.
Density Search Radius
This value specifies the size of the sphere around each points for which other points are included in the density calculation. Normally this value is automatically calculated but one can override it if desired.
Normal Calculation Method
This is a very important option which helps the system align the normals in a consistent way to avoid bubbling problems in the resulting mesh produced. If you have arbitrary point sets the best option here is the default Minimum Spanning Tree. When you have information about how the points are collected the other options may be useful. These options include
None
This is not generally a desirable option as is mostly present to compare doing nothing vs the other option.
Fixed Direction
If you happen to have some knowledge about how the data was collected this can be useful. It lets you choose a primary cartesian axis that all normals should be pointing in. For example say one has data from an arial drone survey. In this case you know all the normals will point pointing in the +ve Z direction so one can select that option and any computed normals that point in -z will be flipped around. This works fine when you have a simple known case like this.
Minimum Spanning Tree
This is the default option and generally works quite well for most data sets. It looks at the nearby point normals and says surfaces won't flip their inside and outside over short distances so it makes sure that normals nearby are all pointing in a consistent direction to avoid this kind of flipping. An option is provided to control how many neighbors to consider in the local field.
QPD Time Based Normals
If one is making a mesh from QPD data, these files know where the source sensor is with respect to the collected points. Thus we can make sure that any points have their normal orientated toward the sensor source. When available this option gives great results and is recommended when using this type of data.
Output Coordinate System
Coordinate Reference System
This field contains the coordinate system the object will be projected in.
Output File
The output filename of the mesh.
Add HIPS Files
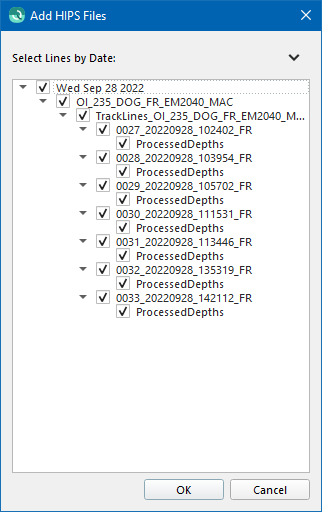
Clicking on the 'Add HIPS Files...' button will bring up a directory selection dialog followed by the Add HIPS Files dialog. Select the desired Lines of HIPS data and hit OK. The selected lines will be added to the Create Mesh Wizard. To add HIPS data, Fledermaus requires a valid CARIS license. To point Fledermaus to the valid CARIS license, refer to the Shared Preference option in the Preference dialog.